Bankroll Management
Now we come to an attribute without which the previous ones count for little: money management. So many punters come unstuck in this area. They find a small number of +EV (expected value) bets, using their encyclopedic knowledge of their chosen sport, only to fall down in this key area. Every bet, unless the result is already known, can lose. Many astute bettors who bet selections at odds against will back more losers than winners. However, good money management and getting value on every selection allows them to turn a profit.
If we consider a player’s bankroll for a second. This is money set aside for betting rather than for life’s necessities. I hesitate to call this money that a bettor can afford to lose, as who can really ‘afford’ to lose their entire bankroll? But it is money set aside solely for betting. Let’s say a punter invests 25% of their bankroll on each of their four carefully researched selections, at Even money. The customer in question makes each selection a true price of 4/5 (or 1.8.) The 25% of bankroll wagered on each bet is crazy.
Even if our bettor is correct in their assumption that each is a 4/5 chance, it is only a 24.63/1 chance that all four selections will lose, leaving our customer with no bankroll remaining (a 4.06% chance of happening.) Even if one selection wins and three lose, 50% of the bankroll will be lost. Should this player want to place three or more selections in the next round of matches at the same price they will need to reduce their original stakes.
A valuable tool when deciding the strength of a wager is the Kelly criterion [1] which is as follows:
f* is the amount that should be wagered
b is the net odds of the wager (b to 1)
p is the probability of the bet winning
q is the probability of the bet losing
If we use the previous example of our bettor who staked 25% of their bankroll on an Even money chance that they believed should have been priced at 4/5, here’s how the Kelly criterion suggests that bet should have been staked:
So, in this example, the Kelly criterion suggests 11.1% of bankroll should be wagered. However, by common consent, Kelly is a very aggressive staking plan and perhaps one-third or one-quarter of the Kelly suggested value is appropriate. What Kelly does help you to do is to decide the correct stakes for very different odds — i.e. an 8/1 shot that should be 9/2, compared to a 5/4 selection that you believe should be 4/5.
Personally, I’d suggest using something akin to one-quarter-Kelly — i.e. the stake should be one-quarter of the amount that the Kelly equation suggests. This reduces the chance of a poor run of results, caused by variance, leading you to lose all or most of your bankroll. In the example above, this would suggest staking either 2.5% or 3% of your bankroll on that bet.
Although different bets on the same market and on the same sport will have differing amounts of an edge, there is a good argument for grouping these at the same stake level. To show a practical application of this, let’s say you bet on the NBA Point Spread. You have recorded your results over a considerable period, and you can see that you have a strike rate of 56% and most of your bets are at 10/11. Using the Kelly criterion with the one-quarter derivation this would suggest that you should bet 1.9% of your bankroll on each selection:
Although you might make some bets stronger plays than others, I’d suggest betting 2% on most plays, but those with a more significant gap between what you make the line and the bookmaker’s price could be stretched to 2.5%, or possibly 3%.
Of course, bookmakers restricting your bets will mean that sometimes you can’t bet the exact amounts that the Kelly criterion would suggest, but at least it acts as a useful starting point.
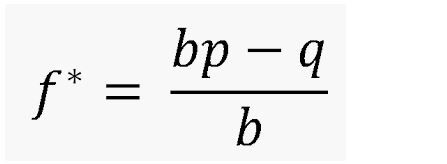


I[1] Kelly, J.L. (1956.) “A New Interpretation of Information Rate.” Bell System Technical Journal. 35 (4): 917-926